What is Group Theory?

So we've been talking about "symmetry operations" and "group theory" and "elements" and such (and if you don't remember, read back a few posts or check out this very helpful video:

Wait...but what exactly is group theory?

Well, in general group theory is just the study of a group of stuff, connected by a central "operation"-- in laymen's terms. More specifically, it explores the relationships among each "element" with respect to each other.

A formal "group" just has elements that have four types of relationships:

1. There needs to be an "identity" operation.

2. When an operation is applied to two elements, the resulting element must also be in the group (Closure).

3. Associativity (just like in math) has to hold.

4. For every element, there has to be an element that, when operated together, result in the identity (inverse).

Woah, that's a lot of complicated jargon. Let's get back to this later.

First, we need to establish which specific group we're talking about, when we refer to group theory in chemistry (again, click on the image to enlarge):

Here is another, nicer way or categorizing these groups:

If this still confuses you, have no fear: An online lecture by Claire Vallance of the University of Oxford provides a simple flowchart that will direct you to the group that you need:

So for the most part, the tables and diagrams above provides a clear definition of what each group stands for. For example, the C1 group refers to molecules without any of the symmetries we talked about before, like this one:

    

This molecule is lysergic acid, with chemical formula C16H16N2O2. Clearly, you can't see any type of symmetry in this molecule-- no reflections, rotations, or inversions are possible...Well, except for the identity (E), which is present in ALL molecules. And so, this group of molecules is rightfully called C1, since C1 is a rotation by 360/1=360 degrees.


Now let's see if each group here meets all of the conditions that we mentioned above! For example, we know that each element has the "E" symmetry, which meets Criterion #1.

Well, long story short, the answer is-- yes! In fact, each group does meet all of these criteria!

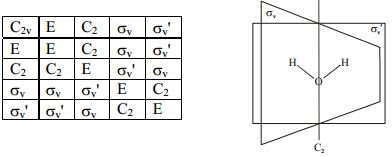
The remarkable thing here is closure: this means that if we do two operations on a molecule, it's equivalent to one operation, which may or may not be different! Let's look at this chart:

As you might have guessed, these are the elements that comprise of the C2v group! This table shows us that if we do two operations (first the column operation, then the row operation), we get an orientation equivalent to one single operation! Pretty cool, huh? This is just the beginning of the wonders of group theory.

One last note: In fact, many of these groups also correspond to the different 3-D shapes in the Valence Shell Electron Pair Repulsion (VSEPR) Theory:

That can't be a coincidence...can it? We leave that as a temporary open question to the reader.