Hello, readers!
For those of you who have traveled with us on our symmetrical journey, we've covered just about all the major topics involving symmetry-- from group theory to fluorocarbons to the ethics behind it all.
We've also encountered several comments and feedback from a couple of experts- such as researcher Dr. Sool Cho, who discussed with us briefly on the matter of whether chemistry-- and specifically symmetry-- is created or discovered. (Thank you again, Dr. Cho! Hope to hear from you again.)
In addition, don't forget about the numerous scientific breakthroughs-- such as the discovery (or creation?) of quasicrystals-- in which symmetry was critical! Indeed, we saw how symmetry really is everywhere around us.
But hold on! We're ending this introductory project, but just the fact that we've touched upon a lot of the topics at hand does NOT mean that our blog will be over! In fact, it's just the opposite. Stick around, as we continue on with our journey.
(In fact, comment! Tell us what you liked about our blogs, or let us know of any symmetric discoveries that we did not mention! After all, the blog is nothing without you all reading.)
Tuesday, March 5, 2013
Wednesday, February 13, 2013
Buckyballs: a spherical perfection?
If you've ever looked at a chemistry textbook, you probably saw a molecule similar to this:
This is actually called a buckyball molecule! Specifically, its name is buckminsterfullerene, and it's comprised of 60 carbon molecules-- and nothing else.
(Did you notice that this exhibits an icosahedral symmetry? Try finding its point group!)
You can see exactly why this molecule made it to our blog-- it's SO symmetric, it almost looks like a perfect sphere!
This is essentially how these molecules were formed:
You can just imagine the countless properties that such a molecule would have. First of all, it's the largest molecule shown to demonstrate wave-particle duality! The discovery of this molecule actually led to a new field of chemistry, which studies JUST fullerenes!
What really intrigued us with this molecule is its attraction to each other in its solid form-- using van der Waals forces! Isn't it surprising, seeing how the molecule is so symmetric? How can they possibly attract each other and stick with each other?
Well, although the molecules are locked against rotation, with a little bit of heating the molecules quickly form face-centered cubics!
Isn't it interesting how even molecules as large and symmetric as these can still attract each other? Very interesting, huh?
This is actually called a buckyball molecule! Specifically, its name is buckminsterfullerene, and it's comprised of 60 carbon molecules-- and nothing else.
(Did you notice that this exhibits an icosahedral symmetry? Try finding its point group!)
You can see exactly why this molecule made it to our blog-- it's SO symmetric, it almost looks like a perfect sphere!
(C60 fullerene solution)
This is essentially how these molecules were formed:
You can just imagine the countless properties that such a molecule would have. First of all, it's the largest molecule shown to demonstrate wave-particle duality! The discovery of this molecule actually led to a new field of chemistry, which studies JUST fullerenes!
What really intrigued us with this molecule is its attraction to each other in its solid form-- using van der Waals forces! Isn't it surprising, seeing how the molecule is so symmetric? How can they possibly attract each other and stick with each other?
Well, although the molecules are locked against rotation, with a little bit of heating the molecules quickly form face-centered cubics!
Isn't it interesting how even molecules as large and symmetric as these can still attract each other? Very interesting, huh?
Sunday, February 3, 2013
The Buck Stops Here
 |
| Neil Degrasse Tyson |
Three words: context is key. We will now zoom out and take a look at symmetry through the eyes of the Synthesis of Symmetry blog we have made, not through the window of one individual post. Occam's Razor states that humans look toward the simplest hypothesis (or the hypothesis that makes the fewest number of assumptions). The human mind craves simplicity. We have three laws of motion, four law of electromagnetism, and physicists today even look for the theory of everything that will encompass quantum mechanics and general relativity. Is this why symmetry is key? Is this why synthesis of symmetry is sought after? Above we have the NaNb3O6 molecule. It self assembles, equally spaced, into black crystals. Arndt Simon and Tony Cheetham and coworkers have synthesized this molecule. This is an example that the chemist Roald Hoffman uses in his essay "Molecular Beauty."
 |
| Immanuel Kant |
What about the age old problem of discovery vs. synthesis? It feels better to create than to discover. This is analogous to the distinction between thermodynamics and kinetics. Now, we are not longer interested in the molecule (the end product) but the process by which we derived the symmetry. To speed up the reaction, there are catalysts. Does the symmetrical properties of these catalyst affect reaction rates? New evidence suggests yes. This example of symmetrical catalysts speeds up asymmetrical reactions. Natural processes are discovered but these catalysts are synthesized. The only conclusion that can be drawn is that synthesis serves to reinforce what is already there.
 |
| Buckminsterfullerene (hard to make) |
 |
| Symmetrical Enzyme |
Tuesday, January 29, 2013
Group Theory-- Culmination!
So in the past couple of posts we've been talking about, among other things, group theory ! Recall that we talked about all of the major point groups and what each group includes. Finally, we'll explore exactly why those are important.
Mainly, group theory immediately answers whether any molecule can or cannot be polar or chiral.
1) Polarity:
Polarity is a subject that we touched upon in a lot of previous posts, and also something that you should be familiar with.
If you look at the H2O molecule above, you will notice that the oxygen atom "hogs up" the electrons within the hydrogen bonds! Thus this molecule-- water-- is polar.
In general, polar molecules will have asymmetric charge distributions-- i.e. some atoms will be more positively or negatively charged than others. This is caused by an intermolecular force called "dipole-dipole" interaction, in which the more positively charged atom(s) tend to pull the electrons closer to themselves, causing a shift in charge and a slight imbalance.
So how does this relate to group theory? Well, if we remember our point group table from before, you'll remember that there are many point groups involving the symmetric property that interchanges the two end-atoms of a molecule-- such groups include Dnd, which include a symmetry plane:
With such even symmetry, it's no surprise that molecules in that group can't have any uneven distributions of charge!
Moreover, if we look at Cn groups, we can see that the dipole moment cannot happen perpendicular to the axis of symmetry-- it's just to symmetric! For example...
If you see that one, it's just too symmetrically formed to share any dipole moments along the axis.
However, that doesn't always mean that Cn can't have any molecules with dipole moments. Take a look below:
For the specific molecule NH3 above, we can see that although there is an axis of symmetry, the molecule is still polar! Geometrically, we can see that all the hydrogens are "pointing down," causing an imbalance of charge.
So in conclusion, the following statement can be made:
Next up:
2) Chirality:
Molecules that are chiral basically has a non-superimposable mirror image molecule.
What does this mean? Well, if you're scratching your head at the confusion, just look at your two hands for a second:
You can easily get from one hand to the other by reflecting it across that mirror plane...But no matter how many translation operations that you try, you won't be able to recreate the other hand.
Now imagine that with molecules...that's what we mean.
This next picture might help clarify more:
Now here's the kicker-- group theory tells us exactly which groups of molecules can't have chiral molecules!
If we think about the symmetry operations, having any mirror planes or centers of inversion would definitely cross out the chances of having chiral molecules, right?
With an inversion symmetry, for example, we know that any "mirror" image molecule can be superimposed using inversion.
And that's not all: the improper rotation can also preclude any chiral molecules:
The picture pretty much sums up the point-- that if a molecule has improper rotation symmetry, then its chirality can also be ruled out.
Therefore, the previous statements can be summed up as the following:
That's it for the very immediate consequences, but don't be fooled! Group theory has implications in chemistry far beyond what we just covered in this post.
So who said that math and chemistry don't mix? Clearly no one who knows about group theory!
Mainly, group theory immediately answers whether any molecule can or cannot be polar or chiral.
1) Polarity:
Polarity is a subject that we touched upon in a lot of previous posts, and also something that you should be familiar with.
If you look at the H2O molecule above, you will notice that the oxygen atom "hogs up" the electrons within the hydrogen bonds! Thus this molecule-- water-- is polar.
In general, polar molecules will have asymmetric charge distributions-- i.e. some atoms will be more positively or negatively charged than others. This is caused by an intermolecular force called "dipole-dipole" interaction, in which the more positively charged atom(s) tend to pull the electrons closer to themselves, causing a shift in charge and a slight imbalance.
So how does this relate to group theory? Well, if we remember our point group table from before, you'll remember that there are many point groups involving the symmetric property that interchanges the two end-atoms of a molecule-- such groups include Dnd, which include a symmetry plane:
With such even symmetry, it's no surprise that molecules in that group can't have any uneven distributions of charge!
Moreover, if we look at Cn groups, we can see that the dipole moment cannot happen perpendicular to the axis of symmetry-- it's just to symmetric! For example...
If you see that one, it's just too symmetrically formed to share any dipole moments along the axis.
However, that doesn't always mean that Cn can't have any molecules with dipole moments. Take a look below:
For the specific molecule NH3 above, we can see that although there is an axis of symmetry, the molecule is still polar! Geometrically, we can see that all the hydrogens are "pointing down," causing an imbalance of charge.
So in conclusion, the following statement can be made:
"The only groups compatible with a dipole moment are Cn, Cnv and Cs."What do we mean when we say "compatible"? We mean that these are the only groups that might have dipole-dipole forces. Particularly, for molecules in Cn or Cnv, we can see that if anything, the dipole has to lie along the axis of rotation.
Next up:
2) Chirality:
Molecules that are chiral basically has a non-superimposable mirror image molecule.
What does this mean? Well, if you're scratching your head at the confusion, just look at your two hands for a second:
You can easily get from one hand to the other by reflecting it across that mirror plane...But no matter how many translation operations that you try, you won't be able to recreate the other hand.
Now imagine that with molecules...that's what we mean.
This next picture might help clarify more:
(The molecule in hand (pun intended) are enantiomers (isomeric pairs of molecules that are chiral) of a generic amino acid.)
Now here's the kicker-- group theory tells us exactly which groups of molecules can't have chiral molecules!
If we think about the symmetry operations, having any mirror planes or centers of inversion would definitely cross out the chances of having chiral molecules, right?
With an inversion symmetry, for example, we know that any "mirror" image molecule can be superimposed using inversion.
And that's not all: the improper rotation can also preclude any chiral molecules:
The picture pretty much sums up the point-- that if a molecule has improper rotation symmetry, then its chirality can also be ruled out.
Therefore, the previous statements can be summed up as the following:
Any molecule with a center of inversion or a mirror plane of any type cannot be chiral. Otherwise, as long as the molecule cannot be improperly rotated, the molecule has the chance of being chiral.
That's it for the very immediate consequences, but don't be fooled! Group theory has implications in chemistry far beyond what we just covered in this post.
So who said that math and chemistry don't mix? Clearly no one who knows about group theory!
Sunday, January 27, 2013
Symmetrical Disease
| That Symmetrical Butterfly |
One rare disease in particular is named symmetrical peripheral gangrene, or SPG. The "normal" version of gangrene can be quite graphic, of course not as graphic as watching Gang Green (a.k.a The New York Jets), as the effected body part loses blood supply and turns a greenish, and eventually black color (for your own sake DO NOT look up pictures of this!). The symptoms involve loss of feeling, confusion, fever, low blood pressure, and an intense pain. A couple of methods of contracting gangrene involve frost bite, surgery, diabetes, or a serious injury. However, the interesting stuff comes with the incredibly rare disease named symmetrical peripheral gangrene. This disease has an incredibly high mortality rate of 40%, and half of the people who survive must have a limb amputation.
| If the left side is affected by SPG, so is the right side |
| Knee Osteoarthritis |
These symmetrical diseases have brought up many interesting questions for doctors and researchers alike. Does a symmetrical bacteria give rise to a symmetrical disease? How can a disease be symmetrical in two separate locations that are quite a distance away. Does the symmetry of the human body play a roll in this? Is the human body even symmetrical? Maybe scientists have to look deeper into the symmetry of the disease and human to realize, along with everyone else, that symmetry is not just that simple butterfly after all.
Wednesday, January 23, 2013
Fluorocarbon
Lets talk about another cool symmetric molecule.
Those two symmetric molecules are both in the group of molecules known as fluorocarbons. Fluorocarbons are basically hydrocarbons, but with all the hydrogen molecules replaced by fluorine. They are colorless and have densities up to twice the amount of water, mostly due to its high molecular weight. When compared to liquids of a similar boiling point, you see that this molecule has low viscosity values. This is due in part to the fact that the only force being applied to this molecule is London Dispersion Force. It also has low surface tension values and a low heat of vaporization. But here is the interesting thing. Because of those low values, this molecule tends to make a very good solvent for gases. Why am I telling you this? Well, because that simple property allows people and animals to do the one thing that has seemed to be beyond our grasp for quite a while, despite being able to such amazing things like getting to the moon. It allows you to breathe in a liquid.
| Perfluorohexane, a stable fluoroalkane liquid |
| Perfluoroisobutene, a reactive and toxic fluoroalkene gas |
Those two symmetric molecules are both in the group of molecules known as fluorocarbons. Fluorocarbons are basically hydrocarbons, but with all the hydrogen molecules replaced by fluorine. They are colorless and have densities up to twice the amount of water, mostly due to its high molecular weight. When compared to liquids of a similar boiling point, you see that this molecule has low viscosity values. This is due in part to the fact that the only force being applied to this molecule is London Dispersion Force. It also has low surface tension values and a low heat of vaporization. But here is the interesting thing. Because of those low values, this molecule tends to make a very good solvent for gases. Why am I telling you this? Well, because that simple property allows people and animals to do the one thing that has seemed to be beyond our grasp for quite a while, despite being able to such amazing things like getting to the moon. It allows you to breathe in a liquid.
| Granted, you will be losing your mind though |
Yep, the picture above is of a hamster losing its mind, while being submerged in a fluorocarbon fluid. And while it does seem to be distressed, it is completely safe(ignoring the side effects). In liquid breathing, the patient is exposed to a perfluorocarbon mixture that has a high oxygen content. Since the mixture is fairly heavy, it sinks to the bottom of the lungs where it opens up the alveoli which leads to the lungs absorbing oxygen. The uses of this material and method is huge. They allow doctors to help people with damaged lungs and sick infants breath. And it would finally allow people to go to extreme depths without the fear of compression sickness and the bends.
By using these flurocarbons, one is able to breath a liquid; a once impossible thought. And while it does have some side effects, it is very amazing what this symmetric particle is able to achieve. Thanks for reading.
By using these flurocarbons, one is able to breath a liquid; a once impossible thought. And while it does have some side effects, it is very amazing what this symmetric particle is able to achieve. Thanks for reading.
Monday, January 21, 2013
A Theory of Knowledge: A Theory of Symmetry
 |
| Why does symmetry appeal to us? |
What do we know and how do we know it? We know babies spend more time gawking at people with symmetrical faces. This symmetry is thus determined by perception and reasoning. Molecular symmetry is significant because it explains data in quantum chemistry, spectroscopy, and crystallography. Chemists view chemistry not as a pinnacle of knowledge but as the median for understanding. Symmetry is the tool, not the birdhouse we all strive to create.
 |
| Symmetrical beauty? |
Is it really ethical to give preference to symmetrical molecules over asymmetrical ones? Is this whole blog sinful and prejudiced? People with symmetrical faces (gauged as more attractive) earn more money for their work according to statistics and that surely is not ethical. We talk about the beauty of these molecules. Cromoglicic acid, shown above, is recognized for its aesthetics by people not even of the science fields. Juxtaposed with the molecule on the left, everyone would rather look at the symmetrical one. Not only this, but the symmetrical one is used for medicinal purposes. Is this suggestive of some connections between altruism and goodwill with symmetry and aesthetics?
There is a clear limit to how symmetrical something can be (perfectly symmetrical) but there is no roof or scale for how asymmetrical something can be. It was mentioned before that things tend to shift to a state of greater symmetry. So is this indicative of symmetry's stance as the promised land? It is basic human nature to favor some things over other simply because of first impressions and this has been proven by analyzing our response to these molecules. I submit to you that human ignorance literally starts at the microscopic level.
Sunday, January 20, 2013
What is Group Theory?
So we've been talking about "symmetry operations" and "group theory" and "elements" and such (and if you don't remember, read back a few posts or check out this very helpful video:
Wait...but what exactly is group theory?
Well, in general group theory is just the study of a group of stuff, connected by a central "operation"-- in laymen's terms. More specifically, it explores the relationships among each "element" with respect to each other.
A formal "group" just has elements that have four types of relationships:
1. There needs to be an "identity" operation.
2. When an operation is applied to two elements, the resulting element must also be in the group (Closure).
3. Associativity (just like in math) has to hold.
4. For every element, there has to be an element that, when operated together, result in the identity (inverse).
Woah, that's a lot of complicated jargon. Let's get back to this later.
First, we need to establish which specific group we're talking about, when we refer to group theory in chemistry (again, click on the image to enlarge):
Here is another, nicer way or categorizing these groups:
So for the most part, the tables and diagrams above provides a clear definition of what each group stands for. For example, the C1 group refers to molecules without any of the symmetries we talked about before, like this one:
This molecule is lysergic acid, with chemical formula C16H16N2O2. Clearly, you can't see any type of symmetry in this molecule-- no reflections, rotations, or inversions are possible...Well, except for the identity (E), which is present in ALL molecules. And so, this group of molecules is rightfully called C1, since C1 is a rotation by 360/1=360 degrees.
Now let's see if each group here meets all of the conditions that we mentioned above! For example, we know that each element has the "E" symmetry, which meets Criterion #1.
Well, long story short, the answer is-- yes! In fact, each group does meet all of these criteria!
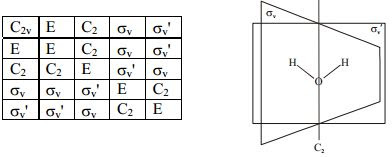
The remarkable thing here is closure: this means that if we do two operations on a molecule, it's equivalent to one operation, which may or may not be different! Let's look at this chart:
As you might have guessed, these are the elements that comprise of the C2v group! This table shows us that if we do two operations (first the column operation, then the row operation), we get an orientation equivalent to one single operation! Pretty cool, huh? This is just the beginning of the wonders of group theory.
One last note: In fact, many of these groups also correspond to the different 3-D shapes in the Valence Shell Electron Pair Repulsion (VSEPR) Theory:
That can't be a coincidence...can it? We leave that as a temporary open question to the reader.
Wait...but what exactly is group theory?
Well, in general group theory is just the study of a group of stuff, connected by a central "operation"-- in laymen's terms. More specifically, it explores the relationships among each "element" with respect to each other.
A formal "group" just has elements that have four types of relationships:
1. There needs to be an "identity" operation.
2. When an operation is applied to two elements, the resulting element must also be in the group (Closure).
3. Associativity (just like in math) has to hold.
4. For every element, there has to be an element that, when operated together, result in the identity (inverse).
Woah, that's a lot of complicated jargon. Let's get back to this later.
First, we need to establish which specific group we're talking about, when we refer to group theory in chemistry (again, click on the image to enlarge):
Here is another, nicer way or categorizing these groups:
If this still confuses you, have no fear: An online lecture by Claire Vallance of the University of Oxford provides a simple flowchart that will direct you to the group that you need:
So for the most part, the tables and diagrams above provides a clear definition of what each group stands for. For example, the C1 group refers to molecules without any of the symmetries we talked about before, like this one:
This molecule is lysergic acid, with chemical formula C16H16N2O2. Clearly, you can't see any type of symmetry in this molecule-- no reflections, rotations, or inversions are possible...Well, except for the identity (E), which is present in ALL molecules. And so, this group of molecules is rightfully called C1, since C1 is a rotation by 360/1=360 degrees.
Now let's see if each group here meets all of the conditions that we mentioned above! For example, we know that each element has the "E" symmetry, which meets Criterion #1.
Well, long story short, the answer is-- yes! In fact, each group does meet all of these criteria!
The remarkable thing here is closure: this means that if we do two operations on a molecule, it's equivalent to one operation, which may or may not be different! Let's look at this chart:
As you might have guessed, these are the elements that comprise of the C2v group! This table shows us that if we do two operations (first the column operation, then the row operation), we get an orientation equivalent to one single operation! Pretty cool, huh? This is just the beginning of the wonders of group theory.
One last note: In fact, many of these groups also correspond to the different 3-D shapes in the Valence Shell Electron Pair Repulsion (VSEPR) Theory:
That can't be a coincidence...can it? We leave that as a temporary open question to the reader.
Sunday, January 13, 2013
Group Theory - Part 2
A few days ago, we began to talk about how math and the concept of group theory came in play with symmetric molecules!
To recap: we assign different types of symmetries with different notations so that we can differentiate one from another easily.
Last time, we talked about three of the 5 main symmetries: The identity, Rotation, and Reflection!
Today we'll talk about the other two:
4) Improper rotation (Sn)
So we know about rotations..but that's an improper rotation?? Well basically, it's a combination of a rotation AND a reflection! Funky right?
As always, it's always best to look at an example:
Here is a ball-and-stick model of methane (CH4). If you look at the two different sides separated by the green plane, you'll notice that we can get to the right side by reflecting it, and then turning it a bit around the green axis! That's the essence behind the improper rotation:
We should note here that, while most molecules with Sn symmetry also have rotational and reflective symmetries, some don't have to! For example, allene (C3H4) has the former but neither of the latter:
You can see how it has S4 symmetry, with the axis through the three carbon atoms and the plane perpendicular to the axis and through the middle carbon. However, it does not have either σ4 or C4 symmetry.
Finally, we arrive at the last (and, to me, the most confusing) symmetry:
5) Inversion (i)
Inversion turns a molecule "inside-out." Basically, if a molecule has inversion symmetry, it has an inversion center. For example, a cube or sphere would have such a center. Similarly, benzene would also have it:
However, other molecules like water don't.
If you're confused, don't worry-- it only gets more complicated.
Having this symmetry would mean that we can arrive at the same molecule by moving each atom of the molecule along a straight line through that inversion center, to a point equally distant from the original position of the atom.
What does that even mean??? Let's find out with an example:
If you see to the right, the ethane molecule has an inversion center, because we can take each of the hydrogen atoms, move it in a straight line through that center, and arrive at one of the other hydrogen atoms!
If that still confuses you, don't worry-- look at the right diagram. In SF6, each fluorine atom moves in line with the center, or the sulfur molecule in this case, and ends up in the position of a different fluorine atom. That's the idea of inversion.
Here are a couple of more examples:
This is a hexacarbonylchromium complex Cr(CO)6. We can clealy see that the center is the Chromium atom, and that each carbon and hydrogen atom can be moved to another of the same molecule.
Easy enough? Well too bad. Here's one that's not so obvious:
This is a staggered 1,2-Dichloroethane (C2H4Cl2) molecule. The center is a bit more hidden in this case, but the picture shows you quite nicely. If you follow the red, dotted line, you'll see that each atom matches the other perfectly. So this has inversion symmetry.
(Also note the S2 symmetry at work here. Coincidence? We encourage the reader to explore.)
Here's where things get funky. Here is eclipsed 1,2-Dichloroethane:
Even though it has the same molecular formula, this one doesn't have the same inversion symmetry! Rather, it has reflective symmetry-- something that the staggered form doesn't have! This tells us that even though molecules may have the same formula, they may have completely different symmetries. We have to be wary of that.
So overall, these are the 5 main symmetries of a molecule: The Identity, Rotation, Reflection, Improper Rotation, and Inversion. This is summed up in the table below:
So, we've finished going over the basics..but now what? Why is this so important? What does this tell us about any properties of the molecule? How can we use this group theory, and what does one symmetry operation have to do with another? We'll continue this journey on a future post.
To recap: we assign different types of symmetries with different notations so that we can differentiate one from another easily.
Last time, we talked about three of the 5 main symmetries: The identity, Rotation, and Reflection!
(Here you can see both the reflection planes and the rotation axis of H2O!)
Today we'll talk about the other two:
4) Improper rotation (Sn)
So we know about rotations..but that's an improper rotation?? Well basically, it's a combination of a rotation AND a reflection! Funky right?
As always, it's always best to look at an example:
Here is a ball-and-stick model of methane (CH4). If you look at the two different sides separated by the green plane, you'll notice that we can get to the right side by reflecting it, and then turning it a bit around the green axis! That's the essence behind the improper rotation:
An Sn improper rotation is a reflection followed by a rotation by 360/n degrees.
So in this case, this would be an S4 improper rotation!
We should note here that, while most molecules with Sn symmetry also have rotational and reflective symmetries, some don't have to! For example, allene (C3H4) has the former but neither of the latter:
You can see how it has S4 symmetry, with the axis through the three carbon atoms and the plane perpendicular to the axis and through the middle carbon. However, it does not have either σ4 or C4 symmetry.
Finally, we arrive at the last (and, to me, the most confusing) symmetry:
5) Inversion (i)
Inversion turns a molecule "inside-out." Basically, if a molecule has inversion symmetry, it has an inversion center. For example, a cube or sphere would have such a center. Similarly, benzene would also have it:
However, other molecules like water don't.
If you're confused, don't worry-- it only gets more complicated.
Having this symmetry would mean that we can arrive at the same molecule by moving each atom of the molecule along a straight line through that inversion center, to a point equally distant from the original position of the atom.
What does that even mean??? Let's find out with an example:
If you see to the right, the ethane molecule has an inversion center, because we can take each of the hydrogen atoms, move it in a straight line through that center, and arrive at one of the other hydrogen atoms!
If that still confuses you, don't worry-- look at the right diagram. In SF6, each fluorine atom moves in line with the center, or the sulfur molecule in this case, and ends up in the position of a different fluorine atom. That's the idea of inversion.
Here are a couple of more examples:
This is a hexacarbonylchromium complex Cr(CO)6. We can clealy see that the center is the Chromium atom, and that each carbon and hydrogen atom can be moved to another of the same molecule.
Easy enough? Well too bad. Here's one that's not so obvious:
This is a staggered 1,2-Dichloroethane (C2H4Cl2) molecule. The center is a bit more hidden in this case, but the picture shows you quite nicely. If you follow the red, dotted line, you'll see that each atom matches the other perfectly. So this has inversion symmetry.
(Also note the S2 symmetry at work here. Coincidence? We encourage the reader to explore.)
Here's where things get funky. Here is eclipsed 1,2-Dichloroethane:
Even though it has the same molecular formula, this one doesn't have the same inversion symmetry! Rather, it has reflective symmetry-- something that the staggered form doesn't have! This tells us that even though molecules may have the same formula, they may have completely different symmetries. We have to be wary of that.
So overall, these are the 5 main symmetries of a molecule: The Identity, Rotation, Reflection, Improper Rotation, and Inversion. This is summed up in the table below:
So, we've finished going over the basics..but now what? Why is this so important? What does this tell us about any properties of the molecule? How can we use this group theory, and what does one symmetry operation have to do with another? We'll continue this journey on a future post.
Subscribe to:
Comments (Atom)