Group Theory-- Culmination!

So in the past couple of posts we've been talking about, among other things, group theory ! Recall that we talked about all of the major point groups and what each group includes. Finally, we'll explore exactly why those are important.

Mainly, group theory immediately answers whether any molecule can or cannot be polar or chiral.

1) Polarity:

Polarity is a subject that we touched upon in a lot of previous posts, and also something that you should be familiar with.

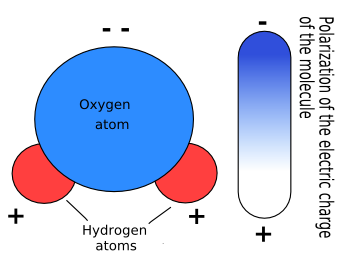
If you look at the H2O molecule above, you will notice that the oxygen atom "hogs up" the electrons within the hydrogen bonds! Thus this molecule-- water-- is polar.

In general, polar molecules will have asymmetric charge distributions-- i.e. some atoms will be more positively or negatively charged than others. This is caused by an intermolecular force called "dipole-dipole" interaction, in which the more positively charged atom(s) tend to pull the electrons closer to themselves, causing a shift in charge and a slight imbalance.

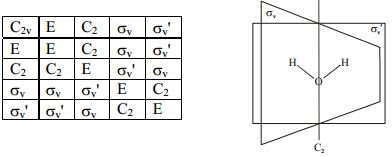
So how does this relate to group theory? Well, if we remember our point group table from before, you'll remember that there are many point groups involving the symmetric property that interchanges the two end-atoms of a molecule-- such groups include Dnd, which include a symmetry plane:

With such even symmetry, it's no surprise that molecules in that group can't have any uneven distributions of charge!

Moreover, if we look at Cn groups, we can see that the dipole moment cannot happen perpendicular to the axis of symmetry-- it's just to symmetric! For example...

If you see that one, it's just too symmetrically formed to share any dipole moments along the axis.

However, that doesn't always mean that Cn can't have any molecules with dipole moments. Take a look below:

For the specific molecule NH3 above, we can see that although there is an axis of symmetry, the molecule is still polar! Geometrically, we can see that all the hydrogens are "pointing down," causing an imbalance of charge.


So in conclusion, the following statement can be made:

"The only groups compatible with a dipole moment are Cn, Cnv and Cs."

 What do we mean when we say "compatible"? We mean that these are the only groups that might have dipole-dipole forces. Particularly, for molecules in Cn or Cnv, we can see that if anything, the dipole has to lie along the axis of rotation.



Next up:

2) Chirality:

Molecules that are chiral basically has a non-superimposable  mirror image molecule.

What does this mean? Well, if you're scratching your head at the confusion, just look at your two hands for a second:

You can easily get from one hand to the other by reflecting it across that mirror plane...But no matter how many translation operations that you try, you won't be able to recreate the other hand.

Now imagine that with molecules...that's what we mean. 

This next picture might help clarify more:

 

 

(The molecule in hand (pun intended) are enantiomers (isomeric pairs of molecules that are chiral) of a generic amino acid.)

Now here's the kicker-- group theory tells us exactly which groups of molecules can't have chiral molecules!

If we think about the symmetry operations, having any mirror planes or centers of inversion would definitely cross out the chances of having chiral  molecules, right?

With an inversion symmetry, for example, we know that any "mirror" image molecule can be superimposed using inversion.

And that's not all: the improper rotation can also preclude any chiral molecules:

The picture pretty much sums up the point-- that if a molecule has improper rotation symmetry, then its chirality can also be ruled out.

Therefore, the previous statements can be summed up as the following:

Any molecule with a center of inversion or a mirror plane of any type cannot be chiral. Otherwise, as long as the molecule cannot be improperly rotated, the molecule has the chance of being chiral. 

That's it for the very immediate consequences, but don't be fooled! Group theory has implications in chemistry far beyond what we just covered in this post.

So who said that math and chemistry don't mix? Clearly no one who knows about group theory!

Symmetrical Disease

That Symmetrical Butterfly

In our blog, we have discussed the connections between symmetry and molecules. However, too many people will respond to a question about symmetry by, not by talking about quasicrystals, but rather mentioning items such as butterflies and trees. This blog post will talk about the real life implications of symmetry, but instead of talking about pretty butterflies, we will dive into the topic of disease. This post will contain relatively few pictures due to the graphic nature of disease, and also the fact that some diseases are not visible to the human eye.



One rare disease in particular is named symmetrical peripheral gangrene, or SPG. The "normal" version of gangrene can be quite graphic, of course not as graphic as watching Gang Green (a.k.a The New York Jets), as the effected body part loses blood supply and turns a greenish, and eventually black color  (for your own sake DO NOT look up pictures of this!). The symptoms involve loss of feeling, confusion, fever, low blood pressure, and an intense pain. A couple of methods of contracting gangrene involve frost bite, surgery, diabetes, or a serious injury. However, the interesting stuff comes with the incredibly rare disease named symmetrical peripheral gangrene. This disease has an incredibly high mortality rate of 40%, and half of the people who survive must have a limb amputation.

If the left side is affected by SPG, so
is the right side

Now the interesting part of this disease comes with the symmetry in its name. Essentially this gangrene affects the extremities on both sides of the body, not just one limb like normal gangrene. Therefore, symmetrical gangrene would be seen on both legs, both feet, or both arms. Being an incredibly rare condition, there has not been much research conducted on the disease, so it is left up to us to hypothesize why symmetry is associated with the disease.  Could it pertain to the bacteria that infect the host? Maybe these bacterium are symmetrical in nature or grow colonies that are symmetrical. However, this would still not explain how the disease is in both limbs considering the large gap in between them. Since humans are known to be symmetrical, should whatever causes the blood vessels to constrict on the left side automatically occur on the right side? This theory seems to make the most sense, but if this is true, there would be no explanation on why this disease is so rare. It should then occur every time one is diagnosed with gangrene. There are many mysteries about this symmetrical disease that are still unsolved, and once scientists have a better understanding of the symmetry, a cure will follow soon after.

Knee Osteoarthritis

A study had been conducted to determine whether osteoarthritis is a symmetrical disease. Osteoarthritis, or OA, is the most common joint disorder that appears due to aging and over use. Some causes of OA are firm cartilage, the breakdown of cartilage  or the development of bone around a joint. As pain and stiffness are some of the worst symptoms of OA, which are MUCH less severe than SPG, (as in you will not die if you have OA), the symmetry in this disease is interesting but you do not  need common sense to determine where the symmetry comes from. The study which was mentioned previously focused on bilateral knee OA and studied patients over a 12 year span to determine if the condition is symmetrical. Now, your probably saying in your head right now: "Well of course this guy is going to find that the disease is symmetrical. If it is caused by wear and tear on a joint, such as running, and you run with two legs, both legs should develop OA". However knee OA is actually considered an asymmetrical disease. This is because each joint is considered its own, single, entity. After the conclusion of the study, it was determined that 80% of people with knee OA have it in both knees. The disease may not occur simultaneously in both knees, but over time, if one develops knee OA, he/ she can expect to get it in the second knee.

These symmetrical diseases have brought up many interesting questions for doctors and researchers alike. Does a symmetrical bacteria give rise to a symmetrical disease? How can a disease be symmetrical in two separate locations that are quite a distance away. Does the symmetry of the human body play a roll in this? Is the human body even symmetrical? Maybe scientists have to look deeper into the symmetry of the disease and human to realize, along with everyone else, that symmetry is not just that simple butterfly after all.

Fluorocarbon

          Lets talk about another cool symmetric molecule.

Perfluorohexane, a stable fluoroalkane liquid

Perfluoroisobutene, a reactive and toxic fluoroalkene gas

       Those two symmetric molecules are both in the group of molecules known as fluorocarbons. Fluorocarbons are basically hydrocarbons, but with all the hydrogen molecules replaced by fluorine. They are colorless and have densities up to twice the amount of water, mostly due to its high molecular weight. When compared to liquids of a similar boiling point, you see that this molecule has low viscosity values. This is due in part to the fact that the only force being applied to this molecule is London Dispersion Force. It also has low surface tension values and a low heat of vaporization. But here is the interesting thing. Because of those low values, this molecule tends to make a very good solvent for gases. Why am I telling you this? Well, because that simple property allows people and animals to do the one thing that has seemed to be beyond our grasp for quite a while, despite being able to such amazing things like getting to the moon. It allows you to breathe in a liquid.

Granted, you will be losing your mind though

     Yep, the picture above is of a hamster losing its mind, while being submerged in a fluorocarbon fluid. And while it does seem to be distressed, it is completely safe(ignoring the side effects). In liquid breathing, the patient is exposed to a perfluorocarbon mixture that has a high oxygen content. Since the mixture is fairly heavy, it sinks to the bottom of the lungs where it opens up the alveoli which leads to the lungs absorbing oxygen. The uses of this material and method is huge. They allow doctors to help people with damaged lungs and sick infants breath. And it would finally allow people to go to extreme depths without the fear of compression sickness and the bends.
      By using these flurocarbons, one is able to breath a liquid; a once impossible thought. And while it does have some side effects, it is very amazing what this symmetric particle is able to achieve. Thanks for reading.

A Theory of Knowledge: A Theory of Symmetry

Why does symmetry appeal to us?

We have spoken a lot about symmetry here on this blog. This blog is concerned with the symmetry of molecules, the building blocks of matter, in particular. But we have never answered the question: why? Why do we care about symmetry? It should be an arbitrary arrangement of molecules like any other. is there something special about symmetry? If one wants to get literary about this, one could argue along the lines of the archetype literary theory. Bear with me for a moment because I am going to proceed to blow your mind by utilizing some components of the IB course, Theory of Knowledge.
What do we know and how do we know it? We know babies spend more time gawking at people with symmetrical faces. This symmetry is thus determined by perception and reasoning. Molecular symmetry is significant because it explains data in quantum chemistry, spectroscopy, and crystallography. Chemists view chemistry not as a pinnacle of knowledge but as the median for understanding. Symmetry is the tool, not the birdhouse we all strive to create.

Symmetrical beauty?

Is it really ethical to give preference to symmetrical molecules over asymmetrical ones? Is this whole blog sinful and prejudiced? People with symmetrical faces (gauged as more attractive) earn more money for their work according to statistics and that surely is not ethical. We talk about the beauty of these molecules. Cromoglicic acid, shown above, is recognized for its aesthetics by people not even of the science fields. Juxtaposed with the molecule on the left, everyone would rather look at the symmetrical one. Not only this, but the symmetrical one is used for medicinal purposes. Is this suggestive of some connections between altruism and goodwill with symmetry and aesthetics?
There is a clear limit to how symmetrical something can be (perfectly symmetrical) but there is no roof or scale for how asymmetrical something can be. It was mentioned before that things tend to shift to a state of greater symmetry. So is this indicative of symmetry's stance as the promised land? It is basic human nature to favor some things over other simply because of first impressions and this has been proven by analyzing our response to these molecules. I submit to you that human ignorance literally starts at the microscopic level.

What is Group Theory?

So we've been talking about "symmetry operations" and "group theory" and "elements" and such (and if you don't remember, read back a few posts or check out this very helpful video:

Wait...but what exactly is group theory?

Well, in general group theory is just the study of a group of stuff, connected by a central "operation"-- in laymen's terms. More specifically, it explores the relationships among each "element" with respect to each other.

A formal "group" just has elements that have four types of relationships:

1. There needs to be an "identity" operation.

2. When an operation is applied to two elements, the resulting element must also be in the group (Closure).

3. Associativity (just like in math) has to hold.

4. For every element, there has to be an element that, when operated together, result in the identity (inverse).

Woah, that's a lot of complicated jargon. Let's get back to this later.

First, we need to establish which specific group we're talking about, when we refer to group theory in chemistry (again, click on the image to enlarge):

Here is another, nicer way or categorizing these groups:

If this still confuses you, have no fear: An online lecture by Claire Vallance of the University of Oxford provides a simple flowchart that will direct you to the group that you need:

So for the most part, the tables and diagrams above provides a clear definition of what each group stands for. For example, the C1 group refers to molecules without any of the symmetries we talked about before, like this one:

    

This molecule is lysergic acid, with chemical formula C16H16N2O2. Clearly, you can't see any type of symmetry in this molecule-- no reflections, rotations, or inversions are possible...Well, except for the identity (E), which is present in ALL molecules. And so, this group of molecules is rightfully called C1, since C1 is a rotation by 360/1=360 degrees.


Now let's see if each group here meets all of the conditions that we mentioned above! For example, we know that each element has the "E" symmetry, which meets Criterion #1.

Well, long story short, the answer is-- yes! In fact, each group does meet all of these criteria!

The remarkable thing here is closure: this means that if we do two operations on a molecule, it's equivalent to one operation, which may or may not be different! Let's look at this chart:

As you might have guessed, these are the elements that comprise of the C2v group! This table shows us that if we do two operations (first the column operation, then the row operation), we get an orientation equivalent to one single operation! Pretty cool, huh? This is just the beginning of the wonders of group theory.

One last note: In fact, many of these groups also correspond to the different 3-D shapes in the Valence Shell Electron Pair Repulsion (VSEPR) Theory:

That can't be a coincidence...can it? We leave that as a temporary open question to the reader.

Group Theory - Part 2

A few days ago, we began to talk about how math and the concept of group theory came in play with symmetric molecules!

To recap: we assign different types of symmetries with different notations so that we can differentiate one from another easily.

Last time, we talked about three of the 5 main symmetries:  The identity, Rotation, and Reflection!

(Here you can see both the reflection planes and the rotation axis of H2O!)

Today we'll talk about the other two:

4) Improper rotation (Sn)

So we know about rotations..but that's an improper rotation?? Well basically, it's a combination of a rotation AND a reflection! Funky right?

As always, it's always best to look at an example:

Here is a ball-and-stick model of methane (CH4). If you look at the two different sides separated by the green plane, you'll notice that we can get to the right side by reflecting it, and then turning it a bit around the green axis! That's the essence behind the improper rotation:

An Sn improper rotation is a reflection followed by a rotation by 360/n degrees.

So in this case, this would be an S4 improper rotation!

We should note here that, while most molecules with Sn symmetry also have rotational and reflective symmetries, some don't have to! For example, allene (C3H4) has the former but neither of the latter:

You can see how it has S4 symmetry, with the axis through the three carbon atoms and the plane perpendicular to the axis and through the middle carbon. However, it does not have either σ4 or C4 symmetry.

Finally, we arrive at the last (and, to me, the most confusing) symmetry:

5) Inversion (i)

Inversion turns a molecule "inside-out." Basically, if a molecule has inversion symmetry, it has an inversion center. For example, a cube or sphere would have such a center. Similarly, benzene would also have it:

However, other molecules like water don't.

If you're confused, don't worry-- it only gets more complicated.

Having this symmetry would mean that we can arrive at the same molecule by moving each atom of the molecule along a straight line through that inversion center, to a point equally distant from the original position of the atom.

What does that even mean??? Let's find out with an example:

If you see to the right, the ethane molecule has an inversion center, because we can take each of the hydrogen atoms, move it in a straight line through that center, and arrive at one of the other hydrogen atoms!

If that still confuses you, don't worry-- look at the right diagram. In SF6, each fluorine atom moves in line with the center, or the sulfur molecule in this case, and ends up in the position of a different fluorine atom. That's the idea of inversion.

Here are a couple of more examples:

This is a hexacarbonylchromium complex Cr(CO)6. We can clealy see that the center is the Chromium atom, and that each carbon and hydrogen atom can be moved to another of the same molecule.

Easy enough? Well too bad. Here's one that's not so obvious:

This is a staggered 1,2-Dichloroethane (C2H4Cl2) molecule. The center is a bit more hidden in this case, but the picture shows you quite nicely. If you follow the red, dotted line, you'll see that each atom matches the other perfectly. So this has inversion symmetry.

(Also note the S2 symmetry at work here. Coincidence? We encourage the reader to explore.)

Here's where things get funky. Here is eclipsed 1,2-Dichloroethane:

Even though it has the same molecular formula, this one doesn't have the same inversion symmetry! Rather, it has reflective symmetry-- something that the staggered form doesn't have! This tells us that even though molecules may have the same formula, they may have completely different symmetries. We have to be wary of that.

So overall, these are the 5 main symmetries of a molecule: The Identity, Rotation, Reflection, Improper Rotation, and Inversion. This is summed up in the table below:

So, we've finished going over the basics..but now what? Why is this so important? What does this tell us about any properties of the molecule? How can we use this group theory, and what does one symmetry operation have to do with another? We'll continue this journey on a future post.

FerroFluids

        Lets talk about something interesting today. That thing is the marvel of ferrofluids. Ferrofluids are basically magnetic particles suspended within a liquid median using a surfactant. This creates a part liquid, part solid substance that displays superparamagnetism. What? Well in much simpler terms, a ferrofluid is a combination of two states of matter. The solid is connected to the liquid using the surfactant, which basically connects the liquid to the solid. A simple example of this is how soap is able to attach oil with water. Besides that, the surfactant is also the thing that is used to keep the magnetic particles from attaching to each other. Now, we reach the biggest word, superparamagnetism. This word simply means that all the particles are so small that they only have one magnetic dipole, meaning they all ether have a south or north pole. Or just a pole in general since you cant have only a south pole. There are a lot of things that can be done with ferrofluids. In fact maybe you have seen one of those cool towers made from them. 

                                     Strangely symmetric aren't they?

And while those things are cool, they don't really have an practical applications. And knowing what the topic of this blog is, lets give an example of some of the interesting symmetrical stuff that is being test about ferrofluids. 

       The first article is titled Effect of MFD Viscosity and Porosity on Revolving Axi-symmetric Ferrofluid with  Rotating Disk. The name may seem complicated, but it is actually quite simple. First, MFD stands for magnetic field-dependent. To start with, when ferrofluid is rotated, it will usually always display y-axis symmetry or axi-symmetric characteristics. Just look at the pictures above if you don't believe me. So, some scientists decided to apply an outside magnetic field to a ferrofluid that was rotating and in symmetry in order to see 3 things. First, how would its viscosity change, its porosity change, and would the ferrofluid even stay symmetrical. While the last tenet doesn't need defining, the first two do. Viscosity is something's willingness to flow. Porosity is the empty space in something. At the end of the experiment, it was found that despite all the variables that were changed the ferrofluids tended to act in a similar manner no matter what. The thing that I take form this however, is that symmetry is very hard to get rid of, no matter the velocity of the spinning, viscosity, or porosity. 

        It is important to remember why this stuff is so symmetric. And just in case you were unable to gather why from the beginning of this post, I will restate it here. Ferrofluids are not just liquids. They have small magnetic solids just floating around in them. And all these things are very easily influenced by a magnetic field. A magnetic field itself, usually goes from north to south. When the ferrofluids are exposed to one, they are go to a position dictated by the field itself. The surfactant keeps them from getting to close, and there you go, constant y-axis symmetry. Thanks for reading. 

The Thermodynamics of Symmetrical Bodies

Boltzmann

Flasks with Cohorts

Albert Einstein's "Electrodynamics of Moving Bodies" did encompass symmetry into some mind blowing theories on space and time and what not. But let us remind ourselves, we are humble people in the pursuit of answers in chemistry. But I do conjure up Einstein's miracle year papers to prove my point of the importance of symmetry.  Boltzmann (the handsome devil whose picture is shown above) had a way to calculate entropy based on the number of macro states a substance (let's say gas) can occupy in a cohort. The flasks with their cohorts are also above. There is a way to calculate entropy; it is S=klnW. S is entropy, k is Mr. Boltzmann's constant, and W is the number of macro states. There is a ubiquitous correlation between symmetry and entropy. Entropy very much is a degree of symmetry. Because there are two types of symmetries( dynamic entropy and static entropy) there are two types of entropies, aptly named dynamic entropy and static entropy. 

Everybody, just relax. I'm going to explain the two. Dynamic symmetry is due to dynamic motion like the motion of one individual molecule and static symmetry is due to phase change. It is obvious, looking at the cohorts, that III has more macro states and greater symmetry (the one that has the statistically better chance at happening). A symmetry increase due to dynamic motion is just as apparent. An electron flying in its orbital leads one to conclude that the hydrogen atom is a symmetrical sphere. If the electron did not move as it did, the atom would not be seen as a sphere because of the definite spot of the electron.  

Change in Gibbs free energy can measure whether some process is spontaneous or not. If it is negative, it is spontaneous, if it positive then it is not, and if it is zero then it is at equilibrium. This is the max entropy. At this state, the substance is most susceptible to some internal or external constraints. Constraints like this include polarity and isotropicity. When these changes happen, because of a force or field, the symmetry is reduced as well as the entropy. Our friends in Basel, Switzerland have come up with the perfect platitude: Any system evolves spontaneously toward a maximal symmetry. It is analogous to saying that when I heat up a gas, the entropy is increased because of the higher number of possible arrangements these molecules can be in. But, contrary to common sense and intuition and thermodynamically speaking, the symmetry increases because individually each molecule has more energy and that little electron is moving a lot faster allowing the nuclei of the molecules to look more like spheres. But there are real irking (I like the work irk) constrains like I just mentioned. The van't Hoff factor (bringing these gas molecules closer together and restricting their degrees of freedom) are the constrains that reduce the symmetry. The point is that that these gas molecules are indistinguishable from one another and that is why the apparent disorder has nothing to do with our discussion on symmetry. I can attest to the fault reasoning that symmetry is disorder. We can say a sphere is perfectly symmetrical because if we rotate it an infinite number of ways, it is distinguishable from all views.  Mathematically, it boils down to this equation: S=lnN! where N! is the total permutation symmetry number.  We have all heard about the heat death of the universe, where the universe (as entropy inexorably increases) will stop at the point where entropy of the universe is maximum. This goes along with the Big Crunch Theory of the death of the universe where the reverse of the Big Bang will happen, essentially. In the fist scenario, the entropy of the universe is max. and in the second, the symmetry of the universe is max. (as everything will be in the singularity). Both are end of universe scenarios (how poetic).  Hope you have enjoyed this look into the relationship between entropy and symmetry (for a while, people have been asking me what's their story, you know are they dating or something but it hasn't been until now that their relationship has been explained in terms of end of time scenarios). 

Symmetrical Hydrogen Bonds v2

In one of our prior posts, we left off without mentioning how symmetrical "hydrogen bonds" are created. We mentioned that "hydrogen bonds" are incredibly strong, but these symmetriacl "hydrogen bonds" are even superior in strength. This post will serve to detail what makes a "hydrogen bond" symmetrical, and how they are formed.

Symmetric "Hydrogen Bond"

Symmetrical "hydrogen bonds" have the potential to be one of the strongest bonds, but what makes a regular "hydrogen bond" symmetrical? A study conducted at Yale University in October of 2012 by Schley involved analyzing iridium (III) alkoxides to determine what gives rise to a symmetrical "hydrogen bond". Utilizing x-ray diffraction, he found, along with his coleagues, that very short hydrogen bonds with O···O distances of 2.4 angstroms exist. After a series of calculations, Shley uncovered that a shorter O···O bond distance will give rise to a symmetrical hydrogen bond.



Symmetrical "Hydrogen Bonds" in Iridium (III) Aloxides

One method which attempts to prove that hydrogen bonds are asymmetric is called the NMR, nuclear magnetic resonance, method. It is illustrated with 3-hydroxy-2-phenylpropenal and then applied to
dicarboxylate monoanions. Resulting from this analysis is that the intramolecular "hydrogen bonds" are asymmetric, although can become symmetric in a crystal structure.


3-hydroxy-2-phenylpropenal

Another article by Charles Perrin states that symmetrical "hydrogen bonds" can occur only in a crystal. He supports this claim by stating that a disorded environment, in solution, will produce an asymmetric bond. However, crystals, such as when water is in its solid phase existing as ice, can guarantee symmetry. So does this mean that symmetric hydrogen bonds can occur only in the solid phase, and never in the gas or liquid phase?


Crystal Structure of Water

A paper entitled "A neutron scattering study of strong-symmetric hydrogen bonds in potassium and cesium hydrogen bistrifluoroacetates: Determination of the crystal structures and of the single-well potentials for protons" demonstrates how "hydrogen bonds" are stronger when in their symmetric, crystalline form. Potassium and cesium hydrogen bistrifluoroacetates emphasize the covalent element of the O···O bond as well as the ionic nature of the hyrogen proton bond. The resulting of this combination of pairing is an incredibly strong bond.


A Hydrogen Bistrifluoroacetates

As a result of these three different studies, we are left with a symmetric "hydrogen bond's" whose strength exceeds that of a regular "hydrogen bond". There are three elements that must be met if we wish for this "hydrogen bond" to be symmetric:

1. "Hydrogen bonding" must occur in the molecule (this is sort of assumed if we are talking about symmetric "hydrogen bonding"
2. The O···O bond distance must be as small as possible
3. The molecule containing the hydrogen bonding should be in a crystal form

Strong Symmetric "Hydrogen Bond"

With all of these conditions met, a regular, rather strong, "hydrogen bond" becomes an incredibly powerful symmetrical "hydrogen bond"



Math? In Chemistry?

As you might have picked up from before, there are several kinds of symmetric molecules! That brings up a huge question-- how do we classify them? How do we differentiate one from another?

Well, that's the purpose of applying group theory in the world of molecules!

Wait a second! Isn't group theory a very advanced mathematical concept? Yes, but it can be applied here in a more simple fashion. This post will cover the basics.

We've touched upon this in one of our earliest blog posts, but it's never bad to repeat something that's so important, right?

In this case, one phrase is crucial to understanding the various types of symmetry:

"A Symmetry operation is an operation which brings an object into a new orientation which is equivalent to the old one."

So for example, in the BF3 molecule below,

we can rotate the shape around the center by 120 degrees. That would change where the atoms go, but it would still maintain the same form. So that rotation would here be a symmetry operation.

There are 5 main symmetry operations involved with molecules:

1) The identity (E)

This is what several people would call a "trivial" operation. Basically, it's doing nothing to the molecule-- that would, of course, keep it in the same form. So every molecule has at least this symmetry operation.

2) Rotation (Cn)

In this operation, we rotate the molecule around certain axes in order to get the same shape back. The axis, depending on the angle that the molecule is rotated by, is called Cn. For example,

as the picture suggests, a rotation by 360/2 degrees around the C2 axis would bring the molecule to the exact same shape! Similarly, rotation by 360/3 degrees around C3 and rotation by 360/4 degree around C4 would both preserve symmetry. 

I hope you realized the pattern: an axis used to rotate the molecule by 360/n degrees is called the Cn axis.

In addition, the operation itself is also called Cn. 

Here are some more examples:

In this famous H2O molecule, we can see that rotating it by 180 degrees around the axis in the middle would make it the same shape! Hence, this molecule has rotational symmetry.

This time, we have something more complicated! There are two different types of rotational axes in this molecule of benzene (C6H6). We can rotate it by 60 degrees around the center C6 axis or by 180 degrees around the C2 axis to get the same hexagonal shape.

Another thing to note here is this-- how many C2 axes do you think there are? I'll give you a moment to think.

Well if you answered 6, you're correct! There are three that intersect through opposite sides-- such as the one shown in the picture, and there are three more that intersect through opposite vertices! That makes 6 whole axes of just C2. This just shows you that a molecule doesn't need to just have one type of rotational symmetry.

Oh, and one more thing-- the Cn axis with the highest value of "n" is called the principal axis.

3) Reflection (σ)

Reflection is also relatively straight forward-- it's just reflecting the molecule across certain planes.

There are three types associated with this symmetry operation: 

          1) Vertical (σv): In this case, the plane of reflection is parallel to the principal axis. Here's an example:

In this ammonia molecule, the plane shown in yellow contains the principal axis. Since reflecting it across that plane would result in the same shape, this molecule is vertically reflective. (That specific reflection is also called σv.)

(If you want to see an interactive, 3-D version of this, click here.)

          2) Horizontal (σh): In this case, the plane is perpendicular to the principal axis. 

Before, we saw that benzene molecules have an C6 rotation axis, which is the principal axis in this case. So the plane shown here would count as the horizontal plane, since it's perpendicular to that axis. And clearly we can see that reflecting the molecule across this plane gets us the same shape. 

          3) Dihedral (σd): This one's a bit more complicated. In this case, the plane is parallel to the principal axis and bisects the angle between two C2 axes. It's best explained with an example:

In this picture, imagine the C2 axes connecting opposite vertices. We see that the plane bisects the angle formed by two of these axes. Since the plane is also parallel to the principal axis, this reflection counts as a dihedral reflection.

Lastly, notice how the dihedral plane was also the vertical plane! The two do not have to be distinct-- rather, all dihedral planes are actually vertical planes, since dihedral planes must also be parallel to the principal axis.

So far, we've covered 3 out of 5 symmetry operations. We'll continue on with our journey at another time.